カナダのベンチャー企業D-Wave社は,D-Wave 2000Qという量子アニーリング専用ハードウェアを開発しました.
組合せ最適化問題を量子アニーリングで解く際は,問題をイジングモデルにマッピングする必要があります.
QUBO (Quadratic Unconstrained Binary Optimization)は,様々なアニーリングマシンで扱える統一フレームワークとして考案されました.
イジング形式とQUBO形式は簡単に変換することができますので,問題をQUBOに定式化しておくと非常に便利です.
イジングモデルのハミルトニアン
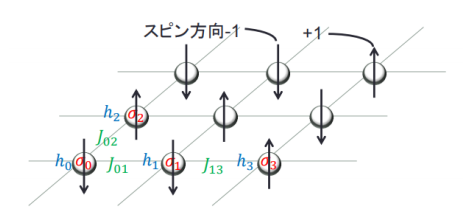
イジングモデル上にマッピングされたノードは,スピン変数として\sigma_i \in \{+1,-1\}どちらかの配位状態を持ちます.
また,ノードi自身にはh_iの磁場係数,ノードiとノードjの間にはJ_{ij}の相互作用係数が存在します.
このモデルのハミルトニアンは,式(1)で表されます.
H=\sum_{i<j} J_{ij} \sigma_i \sigma_j + \sum_i h_i \sigma_i \tag{1}
QUBOへの変換
Nビット変数によるハミルトニアンの最適化を行うには,N \times N上三角行列に係数を定義したQUBO行列を生成することになります.
イジングモデルのハミルトニアンからQUBOを求めるために,\sigma_i \in \{+1,-1\}に対して,q_i = \frac{\sigma_i +1}{2}を作用させます.
これにより,スピン変数\sigma_i \in \{+1,-1\}は,バイナリ変数q_i \in \{0,1\}に変換されます.
さらに,バイナリ変数についてはq_i = q_i^2が成立し,これらを式(1)に作用させることで,式(2)が成り立ちます.
H’=\sum_{i<j} a_{ij} q_i q_j + \sum_i b_i q_i^2 \tag{2}
式(2)はすべての項が,2つのバイナリ変数積で表されます.
よって式(2)は,式(3)のように行列-ベクトル積で表すことができます.
H’=(q_0, q_1, \cdots, q_{N-1}) \left( \begin{array}{cccc} b_{0} & a_{01} & \ldots & a_{0N} \\ 0 & b_{1} & \ldots & a_{1N} \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & b_{N-1} \end{array} \right) \left( \begin{array}{c} q_1 \\ q_2 \\ \vdots \\ q_{N-1} \end{array} \right) \tag{3}
式(3)に表れる上三角行列がQUBO行列です.
実用上は,アニーリングマシンにこの行列を送るだけで済むので非常に便利です.

My favorite food is Sushi and Yakiniku.




コメント