それでは実際に,N対間相互作用について考えていきましょう.
今回も,Vicky Choi (2008)[1]Vicky Choi. Minor-embedding in adiabatic quantum computation: I. the parameter setting problem. Quantum Information Processing, Vol. 7, No. 5, pp. 193–209, 2008.による論文の図を拡張して説明していきます.
N対間相互作用のためのノード複製
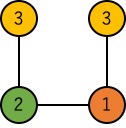
3対間相互作用の場合には,ノード③を2つ追加して,上図のように4ノードで表現することができました.
さらに,ノード④を接続する事を考えます.
一番簡単な方法は,ノード④を必要な分複製し,単純にノード①,②,③のそれぞれに接続すれば良さそうです.
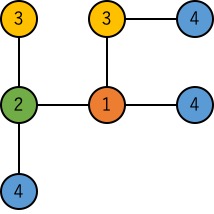
4対間相互作用の場合には,ノード④を3つ追加して,上図のように7ノードで表現することができました.
この辺りから規則性が見えてきましたね!
N対間相互作用に必要なノード数
\(i\) 対間相互作用を実現するために必要なノード数を \(n_i\) 個とします.
\(i+1\) 対間相互作用は, \(i\) 個の既存ノードに新たな接続を設ければ良いので,新たに \(i\) 個の新規ノードが必要となります.
つまり,次の関係式が導けます.
$$n_1=1\tag{1}$$
$$n_{i+1}=n_i+1\tag{2}$$
さらに,式(1)と式(2)を数列漸化式として解くと,式(3)が得られます.途中過程は省略しますが,階差形の漸化式として解くことができます.
$$n_i=n_1+\sum_{k=1}^{n-1}i=1+\frac{(i-1)i}{2}\tag{3}$$
D-Wave 2000Qの限界
式(3)により,イジングモデルでN対間相互作用を実現する際に必要なノード数がわかりました.
それでは,D-Wave 2000Qで,全結合相互作用をいくつ実現できるのか求めていきます.
D-Wave 2000Qは,最大2048量子ビットを利用可能ですので,\(n_i \leq 2048\)となります.
$$1+\frac{(i-1)i}{2} \leq 2048$$
$$i^2-i-4094 \leq 0$$
$$i < \frac{1}{2}+\frac{\sqrt{16377}}{2}=64.486… (0<i)$$
したがって,2048量子ビットで実現できるN対間相互作用は64ビットが最大ということになります.

My favorite food is Sushi and Yakiniku.
References
| ↑1 | Vicky Choi. Minor-embedding in adiabatic quantum computation: I. the parameter setting problem. Quantum Information Processing, Vol. 7, No. 5, pp. 193–209, 2008. |
|---|





コメント